ABSTRACT
Deep geothermal energy systems employ electric submersible pumps (ESPs) in order to lift geothermal fluid from the production well to the surface. However, rough downhole conditions and high flow rates impose heavy strain on the components, leading to frequent failures of the pump system. As down hole sensor data is limited and often unrealible, a detailed and dynamical model system will serve as basis for deeper understanding and analysis of the overall system behavior.
Furthermore, it allows to design model-based condition monitoring and fault detection systems, and to improve controls leading to a more robust and efficient operation. In this paper, a detailed state-space model of the complete ESP system is derived, covering the electrical, mechanical and hydraulic subsystems. Based on the derived model, the start-up phase of an exemplary yet realistic ESP system in the Megawatt range—located at a setting depth of 950m and producing geothermal fluid of 140°C temperature at a rate of 0.145m3 s−1—is simulated in MATLAB/Simulink. The simulation results show that the system reaches a stable operating point with realistic values. Furthermore, the effect of self-excitation between the filter capacitor and the motor inductor can clearly be observed. A full set of parameters is provided, allowing for direct model implementation and reproduction of the presented results.
STATE-SPACE MODEL OF DEEP GEOTHERMAL ESP SYSTEMS
Figure 1. Subsystems and components of an electric submersible pump (ESP) in deep geothermal energy applications (GR = geothermal reservoir)
An overview of the whole ESPsystem, its three subsystems and their components is given in Figure1.
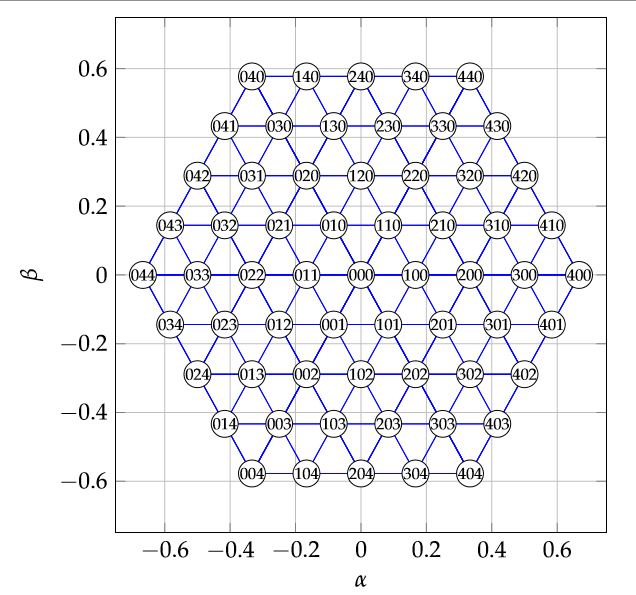
Figure 3. Normalized voltage hexagon (with respect to udc) of a 5-level inverter
In the αβ-reference frame, the feasible phase voltages can be visualized by the voltage hexagon as shown in Figure 3. The respective switching combinations sabc = (sa,sb,sc)T ∈{0,1,2,3,4}3 leading to each node are given in the circles attached to them (e.g., sabc = (2,1,4)T).
Figure 6. Equivalent circuit of the power cable π-segment
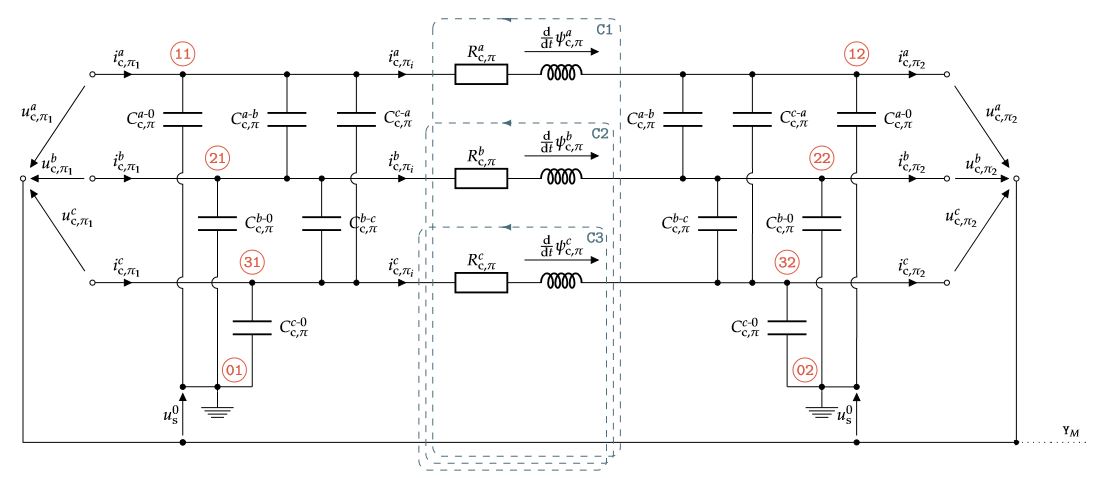
The equivalent circuit of the π-segment is shown in Figure 6, with input voltages uabc cπ1 = (ua c,π1,ub c,π1,uc c,π1)T (in V).
SIMULATION RESULTS AND DISCUSSION
Figure 12. Pump curves of the simulated pump system with trajectories (Hp(·),Qp(·))
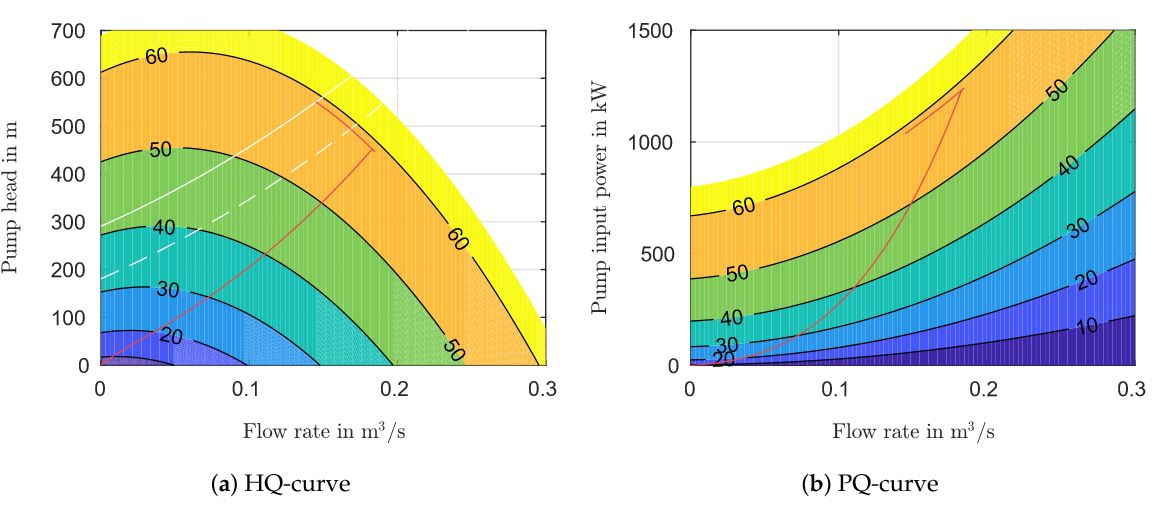
Figure 12. Pump curves of the simulated pump system with trajectories (Hp(·),Qp(·)) (a) and (Pp,m(·),QP(·)) (b) of operating points taken from the simulation data shown in Figure 13
CONCLUSIONS
A detailed state-space model of a deep geothermal ESP system has been derived, comprising the electrical, mechanical and hydraulic subsystems. Moreover, simulations have been performed for a Megawatt ESP system located at 950m below surface level, lifting geothermal fluid of 140◦C temperature. During start-up the electrical frequency has been increased from 0Hz to 60Hz and the voltage amplitude from 0V to 5750V, respectively. It could be observed that—once the start-up procedure was completed—the system reached steady-state, with the pump operating at a constant flow rate of 0.145m3 s−1 and a head of 475m.
Besides reaching stable conditions it could be observed that the cable does not have a significant impact on the system dynamics as the relevant frequencies are located far beyond the fundamental and switching frequencies. On the other hand, the effect of motor self-excitation resulting from the large filter capacitor became apparent when looking at the power factor,reactive power and currents. It should be taken into account when selecting the ESP components, as the motor currents may be considerably higher than the inverter output currents. The mechanical two-mass system between motor and pump showed low-pass characteristics, with the minor torque and speed oscillations from the motor side being almost completely damped on the pump side.
Moreover, simulation results have shown that the model is able to emulate a realistic behavior for the made-up test scenario, the realistic system parameters and the chosen system dimensions. Nevertheless, experimental validation of the overall system or individual sub-systems remains an open task that will be tackled in future work. In this context, a parameter sensitivity analysis should also be conducted in order to identify sensitive parameters of the model. The derived model paves the way for further research steps. For example, it allows to design model-based condition monitoring and fault detection systems which can be implemented on the real time platform to monitor the state of the system online by comparing the model outputs with measured quantities.
In the fault-free case, the deviation is expected to be small provided that the model is correctly parameterized. However, respective action such as a scheduled system shut-down should be taken by the operator, once the error between measurement and model output surpasses a defined threshold. Moreover, state-space observers such as extended Kalman filters or Luenberger observers can be used in order to estimate crucial system states (quantities) which are not measurable or not measured (since additional expensive sensors would be required). The observer outputs substitute measurements, reduce deteriorations due to measurement noise and can likewise be used for more advanced and robust control strategies.
Source: Technical University of Munich
Authors: Julian Kullick | Christoph M. Hackl
>> Matlab Projects Fingerprint Recognition and Face detection
>> 200+ Matlab Projects for Control System for Final Year Students