ABSTRACT
Elliptic curve cryptography (ECC) is one of the most promising public-key techniques in terms of short key size and various crypto protocols. For this reason, many studies on the implementation of ECC on resource-constrained devices within a practical execution time have been conducted. To this end, we must focus on scalar multiplication, which is the most expensive operation in ECC.
A number of studies have proposed pre-computation and advanced scalar multiplication using a non-adjacent form (NAF) representation, and more sophisticated approaches have employed a width-wNAF representation and a modified pre-computation table. In this paper, we propose a new pre-computation method in which zero occurrences are much more frequent than in previous methods.
This method can be applied to ordinary group scalar multiplication, but it requires large pre-computation table, so we combined the previous method with ours for practical purposes. This novel structure establishes a new feature that adjusts speed performance and table size finely, so we can customize the pre-computation table for our own purposes. Finally, we can establish a customized look-up table for embedded microprocessors.
RELATED WORK
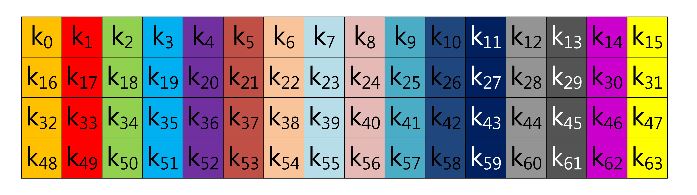
Figure 1. Look-up table structure of Lim and Lee’s method in a block form
In this section, we demonstrate fixed-base scalar multiplication in a block form to allow a comparison of the table structures. In the example, we use a 64-bit scalar value, k, and a look-up table with width-4 index. To illustrate the look-up table index more vividly, we use the same color for the same group elements. Figure 1 shows the structure of Lim and Lee’s method when the width of the block index, (a), is set to 16.

Figure 4. Look-up table structure of the proposed method in a block form for 4NAF
Our proposed method described in Figure 4 represents the scalar value (k) in window-NAF (w). Mohamed et al. grouped values in incremental order of index. On the other hand, we use a different look-up table structure, following the characteristic that the set value in one position will affect the following value’s bit setting.
RESULTS
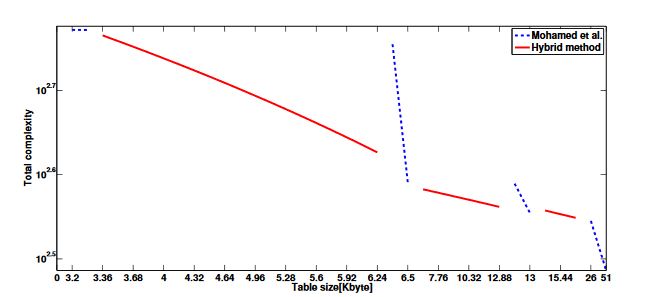
Figure 17. Performance of hybrid model using fine-tuned features
However, the hybrid model using 4NAF is not useful, because zero occurrence of 4NAF is far lower than 3NAF, so even 4NAF has a large table, but shows low speed performance. In Figure 17, a finely-tuned look-up table is depicted. In the figure, we found that with the blue dotted line, the method of Mohamed et al. is coarsely-tuned, so there is a large gap between each look-up table. However, our hybrid model can finely tune and fill gaps between each table, which is coarsely-tuned.
CONCLUSIONS
Recently released novel scalar multiplication by Mohamed et al. reduced the number of addition operations using w-NAF and a novel look-up table structure. However, this method cannot carefully adjust their table structures in terms of speed and size matters, so this does not provide flexibility for selecting table structure, depending on different purposes. In this paper, we presented a novel method for fixed-point scalar multiplication.
The new structure is firstly derived from w-NAF characteristics observed in this paper. However, our method shows similar performance when it is tested under the same look-up table size. However, constructing our table in various ways, we found one interesting features that can be used for speed and size performance adjustment.
Finally, we presented a novel fine-tuned look-up table structure, which can provide more accurate and fine adjustment than previous methods. This idea can be applied to other combinations using many other table structures for the finely-tuned table model. This method can provide more flexible look-up tables for embedded microprocessors.
Source: Pusan National University
Authors: Hwajeong Seo | Hyunjin Kim | Taehwan Park | Yeoncheol Lee | Zhe Liu | Howon Kim