ABSTRACT
In recent years, global navigation satellite system (GNSS)-based navigation in high earth orbits (HEOs) has become a field of research interest since it can increase the spacecraft’s autonomy, thereby reducing the operating costs. However, the GNSS availability and the GNSS-based navigation performance for a spacecraft orbiting above the GNSS constellation are strongly constrained by the signals power levels at the receiver position and the sensitivity.
The simulated level of signal power at the receiver’s position may considerably increase or decrease when assuming different gain/attenuation values of the transmitter antenna for a certain azimuth and elevation. Assuming a slightly different antenna pattern therefore may significantly change the simulated signal’s availability results and accordingly the simulated navigation accuracy, leading to an inexact identification of the requirements for the GNSS receiver. This problem particularly concerns the case of orbital trajectories above the GNSS constellation, where most of the signals received are radiated from the secondary lobe of the transmitters antennas, for which typically very little information is known.
At the time of this study, it was possible to model quite accurately the global positioning system (GPS) L1 antenna patterns for the IIR and IIR-M Blocks because of the precise information available. No accurate information was available for the GPS L1 antenna patterns of the IIF Block. Even less accurate information was available on the GPS L5 antenna patterns. In this context, this paper aims at investigating the effect of different antenna pattern assumptions on the simulated signal availability and on the consequent simulated navigation performance of a spaceborne receiver orbiting in a very highly elliptical orbit from the Earth to the Moon.
Initially the impact of averaging the transmitter’s antenna gain over the azimuth, a typical assumption in many studies, is analyzed. Afterwards, we also consider three different L5 antenna patterns assumed in the literature (the precise L5 patterns are unfortunately not yet fully available). For each of the considered antenna pattern assumptions, we simulate received signal power level, availability, geometric dilution of precision (GDOP), and navigation accuracy in order to evaluate their different effects. After identifying the most conservative assumptions for the transmitters antenna patterns, for each elevation of the receiver antenna, we also compute the number of available GNSS observations and analyze their distribution.
Moreover, possible aiding of the acquisition process using the prediction of the elevation at which the signal is transmitted, as well as the elevation at which the signal is received, are discussed. Finally, the impact on the GDOP of using only signals transmitted from certain angle intervals of the transmitter antenna pattern and the importance of selecting the transmitters that provide the best GDOP (in the case of a receiver with a limited number of channels) are considered and discussed.
MODELS AND ASSUMPTIONS

Figure 3. Assumed MTO for the receiver
For this work, an accurate MTO trajectory of the receiver was generated using the Astrogator Tool of system tool kit (STK), and after provided as reference trajectory in our Spirent simulator, as user motion text (UMT) (user motion) file. The considered MTO is illustrated in Figure 3, where is identified by the yellow curve in LEO and the blue curve in HEO with perigee at the Moon altitude. In this trajectory, a GNSS receiver experiences all signal characteristics that it would experience orbiting at different altitudes in space (from LEO to the Moon).
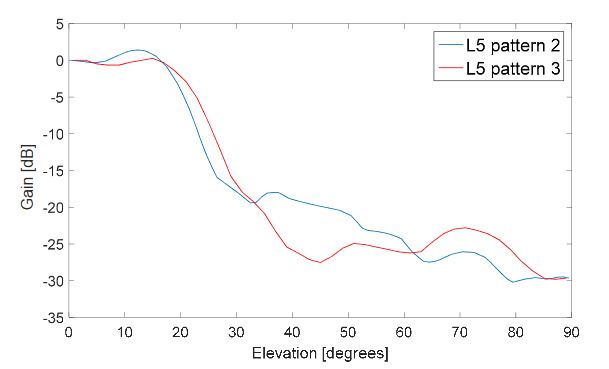
Figure 5. GPS L5 antenna gain pattern
In Figure 5 is shown in blue the assumed L5 antenna gain pattern for the IIF satellites (in the first case) approximated from the L1 antenna gain pattern as explained above, also used in the second case for all GPS satellites. In red we can see the L5 antenna pattern 3.
GLOBAL POSITIONING SYSTEM (GPS) L1 RECEIVER: 2D PATTERN VS. 3D PATTERN
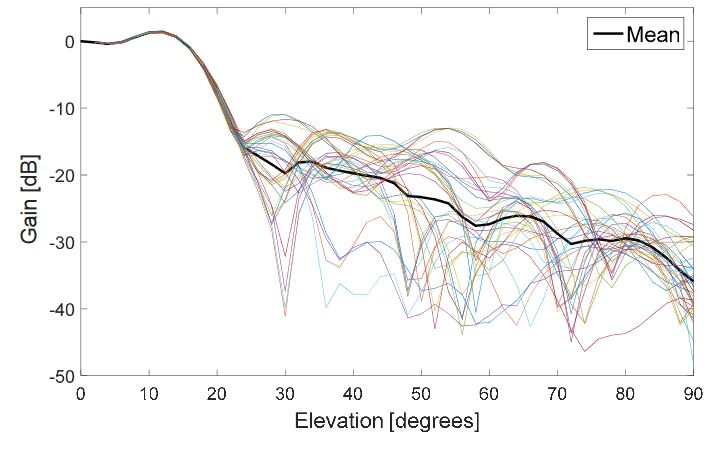
Figure 4. Block IIF GPS L1 antenna gain pattern
The highest received signal powers (Figure 6) are very similar for both assumed patterns, which is explained by the fact that the signal comes from the main lobe of the transmitter antenna pattern; the main lobe patterns are very similar for 2D and 3D patterns, as also shown in Figure 4, because the main lobe pattern is well specified and there is a very small gain variance for different azimuth angles.
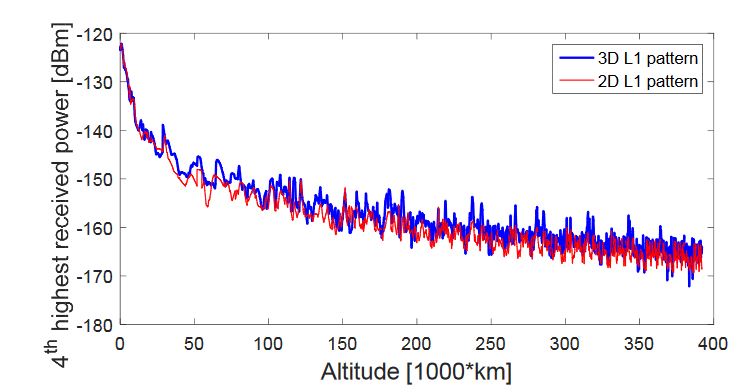
Figure 9. Fourth-highest received power level of GPS L1 signals, during the considered MTO, for a 0 dBi receiver gain pattern
As with four signals we would be able to compute the navigation solution, the fourth received signal power is of highest interest for us. What we can notice from Figure 9 is that in the case of 3D pattern the fourth-highest received signal power is sometimes lower than −170 dBm. On the other hand, this is never the case for the 2D pattern. Observing Figure 9 carefully, we can notice that the received powers are different; however, it is hard to have clear evidence, in which case the received powers are higher.
GPS L1/L5 RECEIVER: L5 PATTERN ASSUMPTION
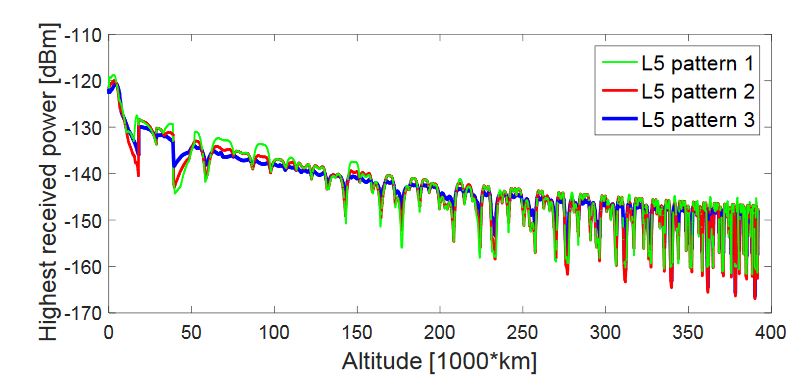
Figure 19. Highest received power level of GPS L5 signals, during the considered MTO, for a 0 dBi receiver gain pattern
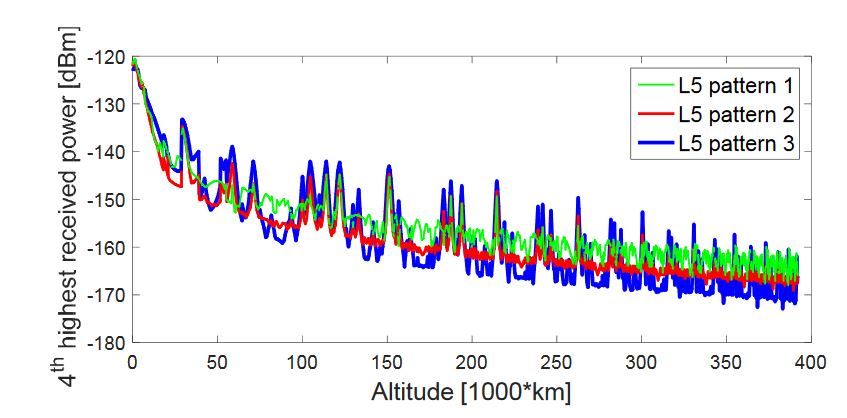
Figure 22. Fourth-highest received power level of GPS L5 signals, during the considered MTO, for a 0 dBi receiver gain pattern
Figures 19–22 show the four highest received power levels of the GPS L5Q signals at the receiver position as a function of the altitude, during the full considered trajectory, when assuming a 0 dBi receiver antenna gain, for the three assumed L5 antenna patterns. As we can see from these figures, the highest and the second-highest received signal powers have similar plots for the three assumed L5 patterns, while the third- and fourth-highest received signal powers plots are more different. From the four figures, we can notice that assuming L5 pattern 1 would result in higher received signal powers, always at the end of the MTO, and also in general for the fourth-highest received power.
NUMBER OF AVAILABLE GLOBAL NAVIGATION SATELLITE SYSTEM (GNSS) OBSERVATIONS FOR EACH RECEIVER ANTENNA ELEVATION
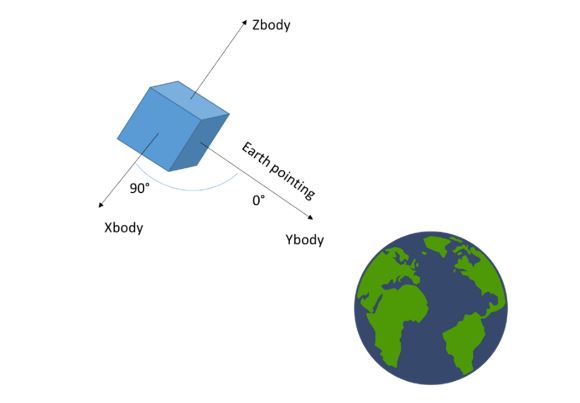
Figure 31. Earth-pointing attitude configuration assumed for the receiver
It is important to highlight that in our simulations, as illustrated in Figure 31, the spacecraft that hosts the receiver is assumed to be pointing towards Earth, with the same body axis always directed towards the earth’s center. Note that this is not the case in a typical lunar mission; however, for the purpose of this analysis (which only aims at investigating the GNSS signals characteristics and the achievable GNSS-based navigation accuracy) it is equivalent to assume that the spacecraft (despite its attitude) will be equipped by one antenna always pointing towards the earth to provide maximum gain. Also note that the elevation is expressed as the semi aperture of a cone, and thus is always positive.
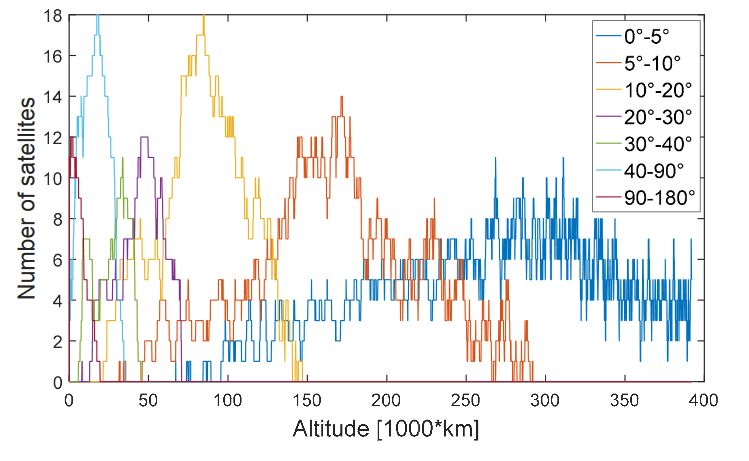
Figure 32. Number of available global navigation satellite system (GNSS) observations for each receiver antenna elevation for each altitude of the whole considered MTO
From Figure 32, we see that above 300,000 km all the signals are received between 0◦ and 5◦, while between 150,000 and approximately 300,000 km there is no available signal at elevations higher than 10◦, which means that above 150,000 km a high directivity antenna pointing towards the earth’s center may be sufficient to process most of the signals.
AVAILABILITY AND ANGLE OF TRANSMISSION FROM THE ANTENNA’S BORESIGHT
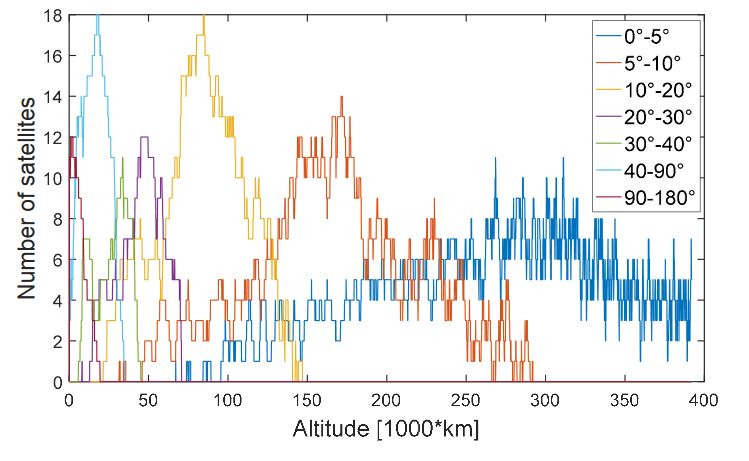
Figure 36. Histogram of the visible satellites (in the line of sight (LOS)) and of the available satellites
Figure 36 displays the histogram of the visible satellites (in the line of sight (LOS)) and of the available satellites (the ones from which the signal transmitted is strong enough to be acquired and tracked by the SANAG receiver) for each transmitter’s antenna elevation during the whole considered MTO. We can see that all the signals transmitted at an elevation angle between 0◦ and 30◦ from the transmitter’s boresight are available, i.e., strong enough to be acquired and tracked by the receiver.
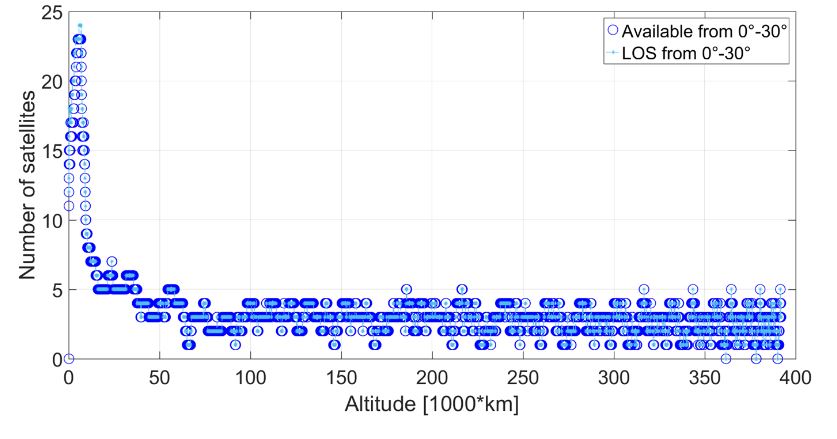
Figure 37. Visible satellites (in the line of sight (LOS)) and available satellites at the receiver’s position
Figures 37–42 show the visible satellites (in the line of sight (LOS)) and the available satellites at the receiver’s position, for which the corresponding signal is transmitted at an angle between 0◦ and 30◦, 30◦ and 37◦, 37◦ and 52◦, 52◦ and 62◦, 62◦ and 75◦, and 75◦ and 90◦, respectively, from the transmitter’s boresight. It can be observed that, if the signal is transmitted between 0◦ and 37◦, it is almost always available at the receiver position, from the beginning to the end of the MTO.
GDOP AND ANGLE OF TRANSMISSION FROM THE ANTENNA’S BORESIGHT
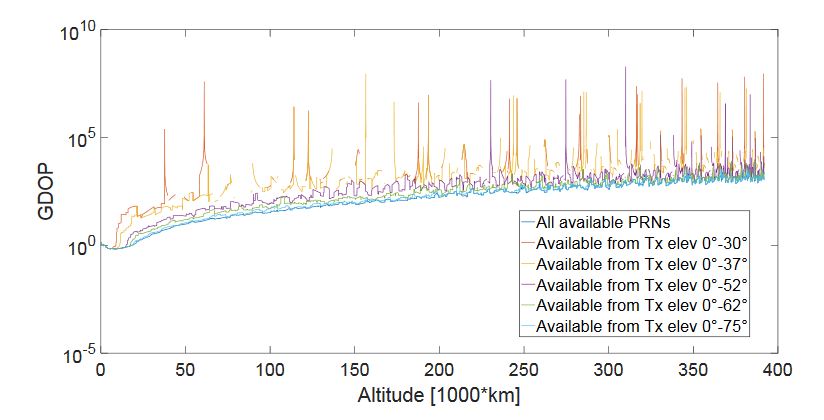
Figure 43. GDOP computed when using all the available signals (each identified by a PRN) and only the ones transmitted
Figure 43 shows the GDOP computed when using all the available signals (each identified by a PRN) and only the ones transmitted at angles between 0◦ and 30◦, 0◦ and 37◦, 0◦ and 52◦, 0◦ and 62◦, 0◦ and 75◦, and 0◦ and 90◦, in order to evaluate what is the relation between the angle at which the signals are transmitted from the GPS satellites and their relative geometry with respect to the receiver.
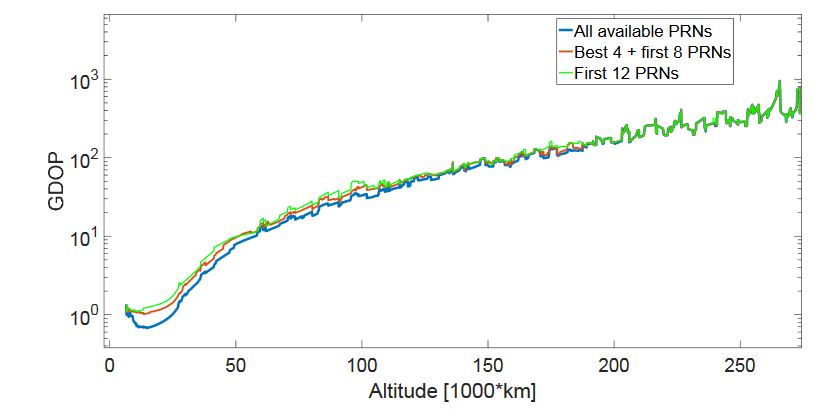
Figure 45. GDOP in three different cases: when all the available signals are processed (in blue), when only the first 12 signals available are processed
For a limited number of acquisition/tracking channels (i.e., the SANAG receiver should have at least 12 channels), in the lower part of the MTO it is not possible to process all the available signals; for altitudes lower than 187,000 km more than 12 signals are available, as shown in Figure 11. Figure 45 displays the GDOP in three different cases. In the best case, all the available signals are processed (see the blue curve in Figure 45).
CONCLUSIONS
In this paper, we investigated the effects of different GNSS transmitters antenna patterns assumptions on the transmitted signals characteristics, in a trajectory that starts from LEO, crossing the SSV and ending at the Moon altitude. In particular, the analysis was carried out by simulating signal power levels, availability, GDOP, code tracking jitter, and, finally, the single-epoch least squares position and velocity solutions, assuming the receiver’s characteristics of the SANAG spaceborne receiver proof-of-concept, under development in our laboratory.
For the transmitters antenna patterns of Block IIR and IIR-M L1 we used detailed information, available in the literature, while we were forced to make an assumption (although conservative) on the L1 IIF Block transmitters patterns. We analyzed the GPS L1 availability in case the assumed patterns vary as a function of elevation and azimuth (3D pattern) and in case they vary only as a function of the elevation (2D pattern). The results show that the variation in the number of satellites is smaller when a 2D pattern is used.
The higher variation in number of available observations when using a pattern changing in both elevation and azimuth causes very big GDOP peaks, which are then reflected in the navigation solution. When the spacecraft is orbiting along the SSV regions only 0.23 satellites per epoch (1s) on average is the difference in availability (with a maximum of two satellites), while above 200,000 km it is 1.24 satellites per epoch (a maximum of five satellites). Hence, the approximation of the antenna gain pattern does not impact the SSV, but mainly very high altitudes.
Authors: Endrit Shehaj | Vincenzo Capuano | Cyril Botteron | Paul Blunt | Pierre-Andre Farine