ABSTRACT
To implement renewable energy resources, microgrid systems have been adopted and developed into the technology of choice to assure mass electrification in the next decade. Microgrid systems have a number of advantages over conventional utility grid systems, however, they face severe instability issues due to the continually increasing constant power loads. To improve the stability of the entire system, the load side compensation technique is chosen because of its robustness and cost effectiveness.
In this particular occasion, a sliding mode controller is developed for a microgrid system in the presence of constant power loads to assure a certain control objective of keeping the output voltage constant at 480 V. After that, a robustness analysis of the sliding mode controller against parametric uncertainties was performed and the sliding mode controller’s robustness against parametric uncertainties, frequency variations, and additive white Gaussian noise (AWGN) are presented.
Later, the performance of the proportional integral derivative (PID) and sliding mode controller are compared in the case of non-linearity, parameter uncertainties, and noise rejection to justify the selection of the sliding mode controller over the PID controller. All the necessary calculations are reckoned mathematically and results are verified in a virtual platform such as MATLAB/Simulink with a positive outcome.
MODELING OF MICROGRID WITH CPL
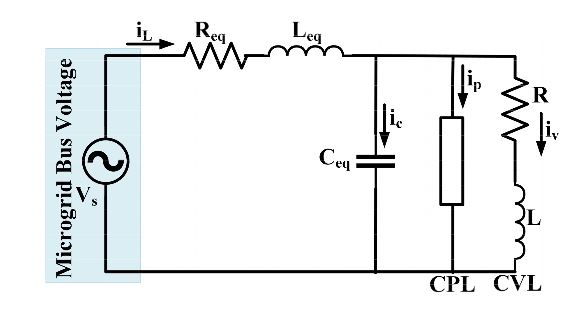
Figure 2. Equivalent circuit of an AC microgrid with CPL and CVL
The small signal equivalent model of the microgrid is represented in Figure 2. Here Vs represents the combined voltage output from the sources of the microgrid. In this paper, source types are not specified and Vs is used as an equivalent of any source that can be used in a practical microgrid. As the renewable sources are intermittent in nature, Vs is modeled as a varying source to simulate that. Req, Leq, and Ceq represent the equivalent transmission line resistance, inductance, and capacitance from source to load. The loads: CPL and CVL, are connected to the transmission line in parallel.
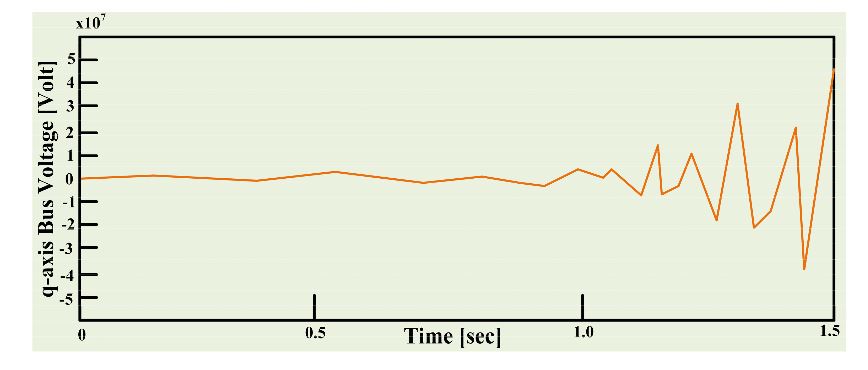
Figure 5. q-axis bus voltage instability due to CPL
In this sequence, the bus voltage instability of q-axis due to the constant power loads is presented in Figure 5. Like the d-axis bus voltage, the exponentially increased signal and random oscillation are also demonstrated in the case of the q-axis bus voltage.
SLIDING MODE CONTROLLER DESIGN
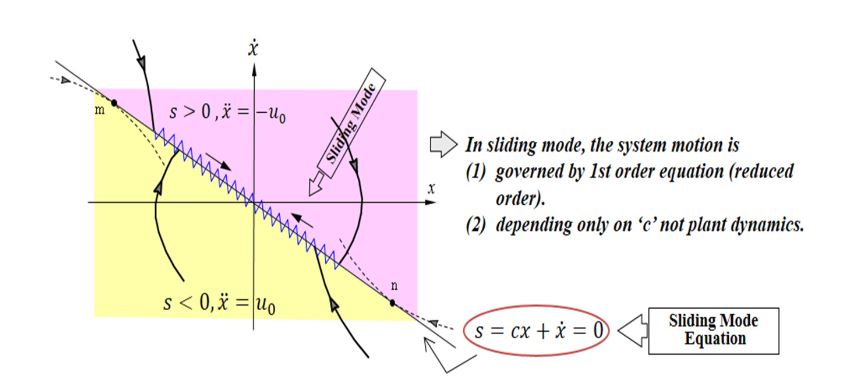
Figure 9. Schematic representation of sliding mode control scheme
Therefore, the SMC can be defined as a variable structured control technique. The certain operation mode of the system, as it slides along the predefined boundaries of the control structures, is called the sliding mode. Besides that, the geometrical locus, necessarily consisting of the boundaries, is said to be the sliding surface of the system. Here, Figure 9 depicts an instance of the trajectory of a certain system regarding the SMC technique. In this illustration, the sliding surface is defined by, s = 0, and, in this occasion, the sliding mode starts after a finite time while the system trajectories have come to the specified surface.
ROBUSTNESS ANALYSIS OF SMC
Our goal is to regulate the output active voltage x3 and reactive voltage x4 by designing the control laws u1 and u2 respectively. As x3 and x4 are related to r1 and r2 through x1 and x2 respectively. So, x1 and x2 are also unknown parameters those satisfy ∆x1 ≤ δx1 and ∆x2 ≤ δx2 for some known bounds δx1 and δx2.
RESULTS
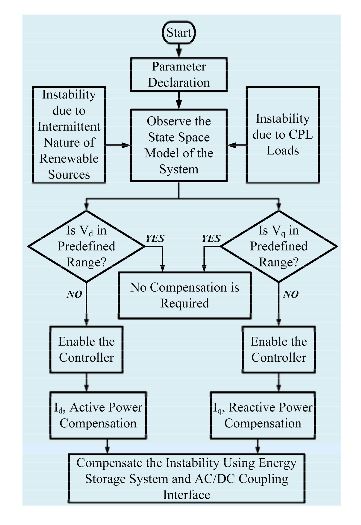
Figure 14. Algorithm for sliding mode control of a microgrid with CPL
Hence, to improve the microgrid stability in the presence of dense CPL, the sliding mode controller is chosen over the PID controller as a load side compensation technique. The algorithm for sliding mode controller simulation platform is presented in Figure 14. In this algorithm, the system is modeled first in state space considering the instabilities caused by intermittency of renewable sources and CPL. If the instability remains within the bounds of a predefined range, no compensation is done.
CONCLUSIONS
Though microgrid systems have several advantages over utility grid systems, to adopt this system for mass electrification is cumbersome due to the CPL instability. To improve the stability scenario of microgrid systems, in this paper, a load side compensation technique has been adopted. Besides a discussion of the previous research work on sliding mode control techniques, a sliding mode controller has been developed for microgrids with constant power loads to assure the control objectives/desired output.
Initially, constant power load instability has been presented with necessary examples. After that, the sliding mode control (SMC) technique has been introduced. Apart from that, the control principle of SMC, chattering, chattering reduction, advantages of SMC, controller design, and the control objectives have been delineated with necessary equations and depictions. Then, a robustness analysis of SMC has been presented in this paper. After that, the results and simulations have been illustrated in the case of a number of system parameters between robustness analysis against parametric variation and robustness analysis against parametric uncertainties, frequency variation and additive Gaussian noise using the SMC control technique based on boundary conditions.
The algorithm of the proposed system has been presented as well. Later, the performance of the PID and the sliding mode controller have been compared in case of non-linearity, parameter uncertainties, and noise rejection to justify the selection of the sliding mode controller over the PID controller. To verify the performance of this approach, simulation results have been demonstrated on a virtual platform such as MATLAB/Simulink.
Source: University of Wisconsin-Milwaukee
Authors: Eklas Hossain | Ron Perez | Sanjeevikumar Padmanaban | Pierluigi Siano
>> 200+ Matlab Projects for Control System for Final Year Students