ABSTRACT
The trajectory design, propellant loading, and staging of a Mars Ascent Vehicle (MAV) can be accomplished via the solution of the associated optimal control problem under given vehicle, mission, path and control constraints. This paper presents the implementation of this optimization using Gauss Pseudospectral Optimization Software (GPOPS-II) in combination with a Sparse Nonlinear OPTimizer (SNOPT) as the nonlinear programing solver.
The solution obtained is an input to the propulsion, Guidance Navigation and Control, mechanical design, aerodynamic and thermal analysis teams, which use it to size systems, tune algorithms and update models. Optimal solutions are obtained for a variety of MAV architectures, which can be grouped in categories according to the number of stages (one or two) and the propulsion technology (solid, liquid or hybrid). A sensitivity analysis of variables of interest, like launch conditions, target orbit, stage and payload mass is presented.
PROBLEM FORMULATION

Figure 1. Optimization setup block diagram
The propellant loading per stage/burn, and the duration of each of the phases in which the ascent is divided; all while satisfying a series of initial, terminal, path and event constraints. The phases and constraints are defined in the following Section. Figure 1 shows the block diagram of the optimization process.
MAV MISSION AND VEHICLE CONSTRAINT
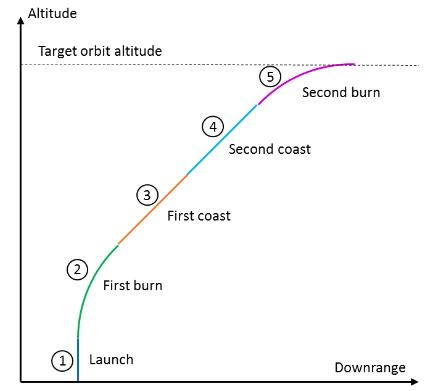
Figure 2. Schematic (not to scale) showing the different phases
We divide the ascent trajectory into five phases: launch, first burn, first coast, second coast and second burn. See Fig. 2 for a graphical description of the phases. The launch phase has a constant duration, typically set by hand, and is a function of the thrust-to-weight ratio of the vehicle: long enough to ensure the vehicle is at least two vehicle lengths in altitude. This is done to ensure adequate clearance from the launch site before closed-loop translational guidance is initiated.
ATMOSPHERIC AND AERODYNAMIC MODELS
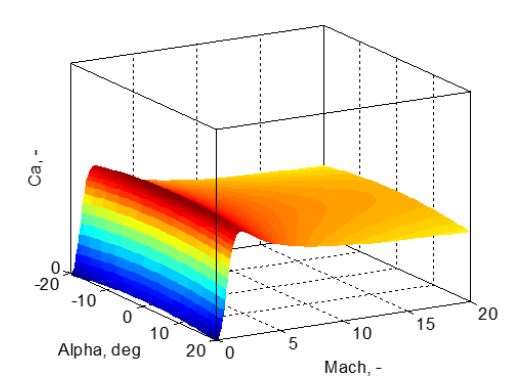
Figure 3. Axial force coefficient for a candidate MAV design
The drag-only aerodynamic model is obtained using Missile DATCOM. Missile DATCOM allows a flexible definition of the vehicle’s geometry and flight conditions explored, making it very suitable to evaluate multiple cases. Given the assumption that the vehicle is axisymmetric, only one axis needs to be explored to characterize the vehicle’s aerodynamics.
RESULTS
The optimization setup is used for 7 different designs (cases) and 6 different subcases. The cases identify different architectures, in number of stages, type of propulsion, dry mass scaling (rubber stretchable tanks or constant) and guidance strategy. The subcases identify choices in payload mass and redundancy policy and choice of avionics. The reader is referred to Ref. for details on the cases and subcases.
SENSITIVITY ANALYSIS
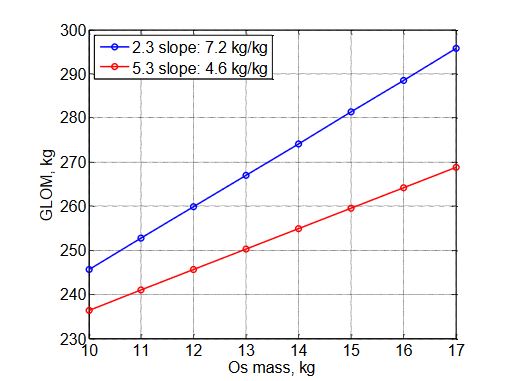
Figure 17. GLOM sensitivity to OS mass
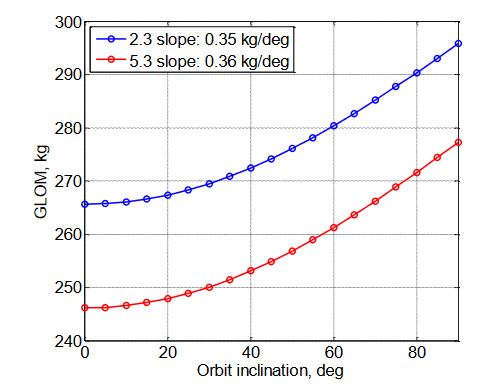
Figure 20. GLOM sensitivity to orbit inclination
A study was performed to evaluate the sensitivity of certain design parameters to some of the output variables, comparing case 2.3 and 5.3 (TSTO vs SSTO). The impact on GLOM is presented in Figures 17-20.
CONCLUSION
This paper describes the approach based on trajectory optimization using GPOPS-II to design and characterize the option space for a MAV. The problem formulation, vehicle and design constraints and models used are outlined, and results for representative cases and subcases are presented. Additionally, a sensitivity analysis of variables of interest is introduced, with the objective to develop rules of thumb to aid mission and vehicle design. The reader is referred to Ref. for additional information and consequences of the results presented in this paper.
Source: University of Michigan
Authors: Joel Benito | Breanna J. Johnson